衰减因子计算器

特别说明：

通过光纤传输的电磁波波长范围通常涵盖可见光和红外光谱，值范围从770 nm到1675 nm。

用于电信的标准单模光纤的核心折射率通常在1.45到1.55之间，而包层的折射率通常在1.44到1.48之间。

多模光纤的核心折射率范围大约在1.48到1.52之间。包层的折射率范围大约在1.44到1.48之间。

衰减因子，α，可以写成，

α的值明显依赖于核心和包层的折射率以及入射角。只有当平方根下的数值为正或大于0时，衰减因子才会有值。

即， 

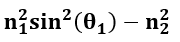
显示为‘结果 1’的值应为正，以便光纤对特定波长具有有效的衰减因子值。

衰减因子

光纤的衰减因子或衰减常数 (α)是用于波传播的参数，用于描述波在介质中传播时振幅或强度减少的速率。它通常用于光学、声学和电磁理论等领域。

当光通过玻璃或光纤电缆等介质时，其强度由于吸收、散射和发散等各种因素而减少。衰减常数量化了通过介质传播的单位距离内强度的减少。

根据比尔-朗伯定律，

其中：

    I是光在介质中距离x处的强度，

    I₀是进入介质的光的初始强度，

    α是衰减常数。

考虑一束光以核心折射率n₁和包层折射率n₂进入光纤。电磁波通过光纤的全内反射（TIR）传播。发生全内反射的必要条件是n₁>n₂。

然后，使用菲涅尔方程和斯涅尔定律，我们可以将强度I表示为，

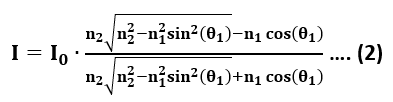
其中：

    θ₁是入射角，

    n₁和n₂分别是核心和包层介质的折射率。

从(1)中，我们可以写出α的方程，

现在从(2)中代入I/I₀的值，我们得到，

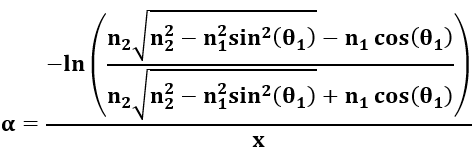
这个α的表达式可能相当复杂，可能没有简单的封闭形式解，因为光与物质的相互作用的性质。然而，在某些情况下或在某些近似下，这个表达式可以简化为，

其中k₀是真空中的波数。波数可以用波长表示为，

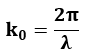
因此，衰减因子α的方程可以写为，